Javascript required
Skip to content Skip to sidebar Skip to footer
Home / Find the Least Squares Solution to 3 Lines

Find the Least Squares Solution to 3 Lines

Problem Set 4: Some Least Squares Solutions

These closely follow the procedures and examples on pages 8--13 of the class Lecture Notes: Vectors and Least Squares

10. Use the Method of Least Squares to find the straight line that best fits the following data given by the points (x,y):

x -2 -1 0 2
y 4 3 1 0

Solution: Step 1.
If the first data point lies on this straight line y=a + bx, then

a + b(-2)=4.
There are similar equations for the other three data points. These give four linear equations for the two unknown coefficients (a, b). Rewriting these four equations in the matrix form AX=Y, we get:

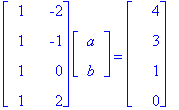
Step 2. Since there are more equations than unknowns, it is highly unlikely that this equation AX=Y has an exact solution. Instead, using the Method of Least Squares we seek a solution X that minimizes the error ||AX-Y||. As we saw, this leads us to solve the normal equations A*AX=A*Y. We already proved in class that the adjoint of A is the transpose of A (that is, A* = AT). Therefore the normal equations are: ATAX = ATY. In detail:

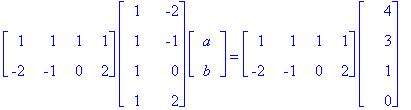
After doing the computation this is just

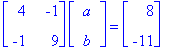
Step 3. We have 4a - b = 8 and -a + 9b = -11. This is a simple linear equation whose solution is
a = 61/35 and b = -36/35.
Thus, the equation of the desired straight line is:
REMARK: In real life, after Step 1 one should immediately use a computer package such as Maple to carry out the details. This becomes even more significant in more complicated problems.
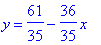
11. The water level in the North Sea is mainly determined by the so-called M2 tide, whose period is about 12 hours. The height H(t) thus roughly has the form
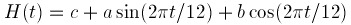
<center> H(t) = c + a sin (2 pi t/12) + b cos(2 pi t/12), </center>

where time t is measured in hours. Say one has the following measurements:

t (hours) 0 2 4 6 8 10
H(t) (meters) 1.0 1.6 1.4 0.6 0.2 0.8

Use the method of least squares with these measurements to find the constants a, b, and c in H(t) for this data.

Solution: The same method applies as in the previous problem. Ideally we would like the six data points to satisfy the equation

y = c + a*sin(Pi*t/6) + b*cos(Pi*t/6)

Rewrite these six equations in the three unknowns (c, a, b) as a matrix equation: AX = Y.

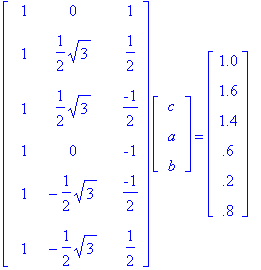
To solve for the X giving the smallest error ||AX-Y||, we solve the normal equations: A*AX = A*Y. This is best done using a computer. Proceeding by hand we get

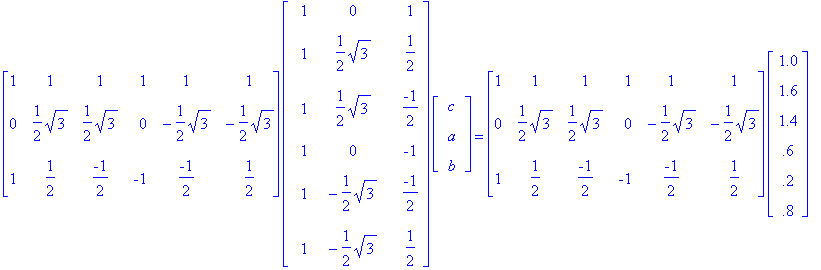
that is,

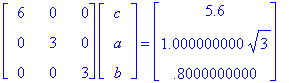
Solving these we find that 3a = sqrt(3), 3b = 0.8, and 6c = 5.6. Therefore
a = sqrt(3) /3,   b = 4/15,   and   c = 14/15.

The resulting formula for y=H(t) is:
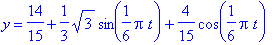
12. Find a plane of the form
z = ax + by + c

that best fits the following five points: (0, 0, 1.1), (1, 1, 2), (0, 1, -0.1), (1,0,3), (0, -1, 2.1).

Solution: This is very similar to #10, except now there are five equations for the three unknowns (a, b, c). A computer package such as Maple makes this simple.

13 a). Some experimental data (x_i, y_i) is believed to fit a curve of the form
y = (1+x)/(a + bx2),
where the parameters a and b are to be determined from the data.
The method of least squares does not apply directly to this since the parameters a and b do not appear linearly. Show how to find an equivalent equation to which the method of least squares does apply.

Solution: Multiply the equation by a + bx2 to get the equivalent equation

ay + bx2y = 1+x.
This equation is linear in the unknown coefficients a and b, so the method of least squares applies.

Find the Least Squares Solution to 3 Lines

Source: https://www2.math.upenn.edu/~kazdan/210/210F06/hw/solns/hw4solns.html