Dynamic Programming Solution to Finding the Combination
Quick Guide to Dynamic Programming
Finding the optimal solution by breaking it down into smaller problems doesn't have to be hard
![]()
Dynamic programming is a general method to solve optimization problems ("find the maximum/minimum/shortest/longest…") by breaking them down into smaller ones ("divide and conquer") and keeping track of their solutions ("memoization") to make a more efficient use of information and resources. Memoization can be seen as a form or recursion. If you find it confusing, it's probably because you don't understand why it's called "dynamic" in the first place. It turns out that the name is deliberately misleading for a historical reason.
A Simple Example
Let's say you want t o calculate 6 x 2. Of course, you can expand the multiplication into a series of additions, such as:
6 x 2 = 2 + 2 + 2 + 2 + 2 + 2
There certainly are many ways to carry out the sum. For example:
6 x 2 = (2 + 2) + 2 + 2 + 2 + 2 = (4 +2) + 2 + 2 + 2 = (6 + 2) + 2 + 2 = (8 + 2) + 2 = 10 + 2 = 12
There's nothing wrong with this solution, but the point is, every addition is a new case (as highlighted by the boldface font). Is there another way so that we can "recycle" information about sub-problems? Indeed, we can rewrite the sum as…
6 x 2 = (2 + 2) + (2 +2) + (2+2) = (4 + 4) +4 = 8 + 4 = 12
As you can see, in the intermediate step the trick is basically to calculate (2+2) only once, and store its result into memory. Whenever we encounter (2+2) again, we don't have to calculate the result, but just fetch it from memory. It doesn't really matter for such a simple example, for in real situations obtaining the result of a sub-problem may be time- or memory-consuming, hence this approach may have huge advantage over alternative methods. That's the essence of dynamic programming. To recap, the steps usually are:
- Break down the problem into smaller sub-problems;
- Figure out a formula to build larger problems from smaller ones;
- Find the solution for the smallest one;
- Create a table to keep track of the smaller solutions;
- From the smaller solutions, build up the final answer.
The {0,1} Knapsack Problem
In this optimization problem, one has a list of N items with an associated weight w[i] and value v[i], and a "bag" with maximum capacity W. The goal is to find the subset of the items such that the total value is maximum and the sum of weights is less than W. In this simplified version of the problem, items can either be picked up or not, but not fractions or multiples of them, hence the {0,1} in the definition. From elsewhere, you might have seen the example of a burglar breaking into Bill Gates' house, trying to steal as much stuff as possible. A less dramatic example may be getting ready for a hiking trip: you want to bring some useful items with you, but you don't want to be overwhelmed by their weight either.

If you don't know where to start from and the problem has a few items, a brute-force or "exhaustive search" approach may do the trick. That is, try all possible combinations of items and calculate the total weight and value of all subsets. Select the one that satisfies the requirement. It turns out this approach has an exponential time complexity of O(2^N). However, noting that many smaller combination of items appear multiple times, this should be an indication that dynamic programming is likely to be a more efficient way to solve the problem.
The logic follows a bottom-up approach. Let's pick up a given item i. If its weight w[i] is larger than the maximum capacity of the knapsack W, it can't be part of the solution. On the other hand, if w[i] < W then it might be part of the solution. Thus, we need to explore two possibilities:
- One where we find the optimal combination without item i.
- One with item i, plus the optimal combination of other items. In this case, the total weights of the remaining items must be smaller than W-w[i] or it won't satisfy the constraint (too heavy).
You see that the recursion involves looking into smaller combinations while keeping item i in the knapsack. Also, there may not be any viable solution! To solve the problem in practice, we need a 2D table where rows refer to items and columns to the maximum weight (in the implementation below, weights are "quantized" to integers). The table needs an additional row to handle the case with no items. Here follows a simple implementation in python3:
The expected result is 25. Also, you'll notice that many entries in the table are None, i.e. the default value. That's because the algorithm never encounters a certain combination which weight corresponds to that column. If you change the initial values of weights and values you may see different results.
Dynamic Programming and Reinforcement Learning
The Dynamic Programming approach plays an interesting role in a branch of Artificial Intelligence called Reinforcement Learning (RL), where an entity has to learn to explore the environment to find the path that maximizes a reward. You have probably seen examples of a computer playing classic videogames. While we're not delving into the intricacies of RL, you can easily understand part of the exploration aspect of it is likely to involve finding the shortest path that maximizes or minimizes some cost function.
A simple example is given by a robot living in a chessboard, whose goal is to start from let's say the top-left corner and get to the bottom-right corner, moving only in straight lines and making only right-angle turns. Before we even make a move, we may ask how many unique paths are there. Once we have solved this problem, we may decide for example to explore only some of them, but that goes beyond the scope of this post.
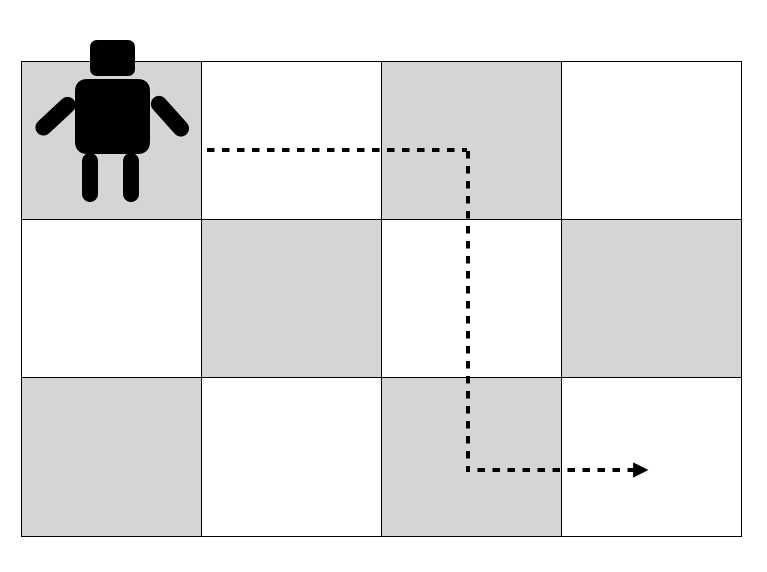
To solve the problem, once again we create a 2D table to keep track of how many times a given square has been visited. In this case, if the chessboard has m rows and n columns, the table has dimension (m+1) x (n+1) to account for the base cases. The idea is that for each row, the robot can go up to the last column then make a turn and continue all the way to the target, or stop to the column n-1 make a turn and then continue on the row below. But at this point, the number of available rows and columns has decreased, so that corresponds to a smaller, sub-problem. Eventually there will be only one square left (the target) and that's the stopping condition.
Here's a simple implementation that works with python3:
With the inputs above (m=3, n=4), the result should be 10. To be fair, this case is relatively simple and could have been solved without recursion. Here's an example:
Finally, the more math-prone readers might have also noticed that the answer to the problem can be found by simply reasoning in terms of the number of combinations with repetitions of m rows and n columns. The robot has to get to the target in m-1 right and n-1 down movements irrespective of the order. That is a one-liner involving a factorial:
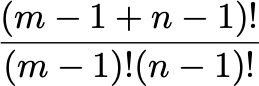
Conclusions
Dynamic Programming is a very powerful optimization method which applications that go far and wide. I think it's interesting to see how a method developed in an era where computing resources were extremely limited is still finding newer and newer applications in fields such as Reinforcement Learning that were considered almost sci-fi back then.
Dynamic Programming Solution to Finding the Combination
Source: https://towardsdatascience.com/quick-guide-to-dynamic-programming-c1618698d341